Månen forbliver jo ikke over det samme sted på jorden hele tiden (den er ikke geostationær), og jorden roterer jo også om sin egen akse, derfor "varer" solformørkelsen et bestemt stykke tid. 

For at beregne skyggens hastighed over jorden er der en del faktorer vi må tage højde for, derfor kommer der i det følgende en masse data, samt ind i mellem en del udregninger, der skal give os nye data, da alle de informationer vi har brug for ikke er umiddelbart tilgængelige. Vi har fundet de nedenstående data i vores fysikbog (der godt nok hører til obligatorisk niveau, men har alle de relevante oplysninger) og et atlas. 
 

Data om månen:
Omløbstid	27,322 døgn
Afstand fra jordens centrum	384.399 km	NB. Middelafstand

Således kan månens banelængde bestemmes idet vi forestiller os at banen er en cirkel (i virkeligheden er det en ellipse). Omkredsen O på en cirkel har formlen 

Nu kan vi regne månens hastighed ud. Hastighed måles oftest i km/t, men i fysik er det rart at bruge m/s, da meter og sekund er grundenheder. Her vil vi dog regne i km/t. Månens hastighed v bestemmes så ved 

Omløbstiden skal være i timer, da vi ønsker at få enheden km/t, men vi kender den kun i døgn. Men vi ved at der er 24 timer på et døgn, så på 27,322 døgn er der 

Månens hastighed bliver så: 

Det bliver altså ca. 3700 km/t, samtidig med at månen farer rundt om solen sammen med jorden. Det er lidt skægt at tænke sig, at der flyver en klump på 73.480.000.000.000.000.000.000 kg (73 milliarder billioner kilogram) rundt om jorden med 3700 km/t. Jordens hastighed vil vi starte med at finde ved Karlsruhe i Tyskland, hvor vi oplevede solformørkelsen. Derfor skal vi bruge nogle oplysninger om netop dette sted på jordkloden: 

 
 

Data om Karlsruhe
Breddegrad	49°
Jordens radius	6.378,137km

Det vi nu ønsker at bestemme er jordens omkreds ved Karlsruhe, som det ses på nedenstående tegning: 

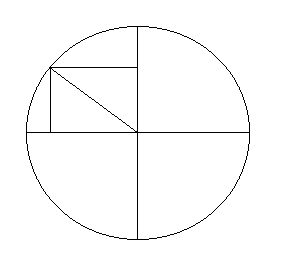
På tegningen er r radius for den cirkel hvis omkreds vi vil bestemme, men vi kender ikke r. Derimod kender vi R, som er jordens radius. Det er både den vandrette streg, men også den skrå streg fra centrum af cirklen til Karlsruhe. b (vinkel b) er breddegraden ved Karlsruhe. Så ses det at Karlsruhe, jordens centrum (cirklens centrum) og punktet a danner en retvinklet trekant. Der gælder nogle regler for sammenhængen mellem vinkler og sider i trekanter (disse er beskrevet i trigonometrien) og særligt gælder det for retvinklede trekanter at: 

Vinklen vi er i er b ved Karlsruhe. Det er nu nemmest at forestille sig at man står inde i vinklen med ryggen til Karlsruhe og kigger ud. Den hosliggende side er så r og hypotenusen er R. Ved en omskrivning kommer vi frem til 

Vi kender formlen for en cirkels omkreds, den er beskrevet ovenfor, så vi kan nu finde ud af, hvor langt der er rundt om jorden langs breddegraden ved Karlsruhe. 

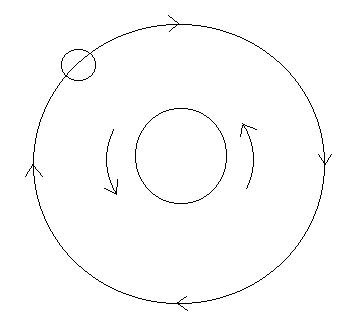
På tegningen ses det at Jordens spin om dens egen akse har samme retning som Månen rundt om Jorden. Derfor skal Jordens hastighed trækkes fra Månens hastighed. Derfor vil vi nu finde jordens hastighed ved Karlsruhe, hvor vi jo kender omkredsen og vi ved hvor lang tid det tager jorden at dreje rundt om sig selv, nemlig 23 timer 56 minutter og 4,103 sekunder - normalt siger man 24 timer, men vi vil her regne med den anden omløbstid, som i timer er 23,934t. Hastigheden ved Karlsruhe kommer så her: 

Så trækkes Jordens hastighed fra Månens hastighed. Måneskyggens hastighed ved Karlsruhe, som vi her finder frem til, kalder vi S: 

Den måneskygge vi så ved Karlsruhe bevægede sig altså med ca. 2600km/t, eller med samme hastighed som en Concorde (verdens hurtigste passagerfly) - heldigvis er Månens skygge på Jorden noget større end en Concorde, så derfor varer en solformørkelse længe nok til at man kan opleve den. På samme måde kan man regne hastigheden for måneskyggen ved København ud. Den ville selvfølgelig kun være der, hvis der var total solformørkelse i København, men der går næsten 500 år før det sker igen. Når det sker vil måneskyggens hastighed være ca. 2750 km/t.