


Next: Results on IBM
Up: Parallel ab-initio molecular dynamics
Previous: Car-Parrinello ab-initio molecular
Given the virtually unlimited need for computational resources required
for studying large systems using ab-initio molecular dynamics, it
is obvious that parallel supercomputers must be employed as vehicles
for performing larger calculations. Parallel Car-Parrinello
implementations were pioneered by Joannopoulos et al.[8]
and Payne et al.[9], and by now several parallel codes are
being used[10,11].
The parallelization approaches for the Car-Parrinello algorithm focus
on the distribution of several types of data[10]: 1) the
Fourier components making up the plane wave eigenstates of the system,
and 2) the individual eigenstates (``bands'') for each k-point of the
calculation. The first approach requires the availability of an
efficiently parallelized 3D complex FFT, whereas the second one does
the entire FFT in local memory, but needs to communicate for
eigenvector orthogonalization.
The selfconsistent iterations require that a sum over the electronic
states in the system's Brillouin-zone be carried out. For very large
systems, and especially for semiconductors with fully occupied bands,
it may be a good approximation to use only a single k-point (usually
k = 0) in the Brillouin-zone, and this is done in several
of the current implementations.
However, it is our goal to treat systems that consist only of a few
dozen atoms, and which typically consist of transition metals with
partially occupied d-electron states. This requires rather large
plane wave basis sets, as well as a detailed integration over the k-points \
in the Brillouin-zone, in order to define reliably the band occupation
numbers of states near the metal's Fermi surface. Hence we
typically need to use about a dozen k-points .
With such a number of k-points , and given that many parallel
supercomputers consist of relatively few processors with rather much
memory (128 MB or more), it becomes attractive to pursue a
parallelization strategy based upon farming out k-points to
processors in the parallel supercomputer. Since traditional electronic
structure algorithms have always contained a serial loop over k-points ,
each iteration being in principle independent of other iterations, this
is a much simpler task than the other two approaches referred to
above. This approach is not any better than the other approaches,
except that it is well suited for the problems that we are studying,
and it could eventually be combined with the other approaches
in an ultimate parallel code.
The parallelization over k-points is in principle straightforward. If we
for simplicity assume that our problem contains N k-points and we have
N processors available to perform the task, each processor will
contain only the wavefunctions (one vector of Fourier components for
each of the bands) for its own single k-point . A very significant memory
saving results from each processor only having to allocate memory for
its own k-point 's wavefunctions (in general, 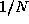 -th of the k-points ). The
wavefunction memory size is usually the limiting factor in
Car-Parrinello calculations. A number of tasks are not inherently
parallel: a) Input and output of wavefunctions and other data from a
standard data file, b) accumulation of k-point -dependent quantities such
as charge densities, eigenvalues, etc., c) the calculation of total
energy and forces, and the update of atomic positions, and d) analysis
of data depending only upon the charge density. These tasks should be
done by a ``master'' task.
-th of the k-points ). The
wavefunction memory size is usually the limiting factor in
Car-Parrinello calculations. A number of tasks are not inherently
parallel: a) Input and output of wavefunctions and other data from a
standard data file, b) accumulation of k-point -dependent quantities such
as charge densities, eigenvalues, etc., c) the calculation of total
energy and forces, and the update of atomic positions, and d) analysis
of data depending only upon the charge density. These tasks should be
done by a ``master'' task.
We have chosen to implement parallelization over k-points by modest
modifications of our existing serial Fortran-77 code. Using
conditional compilation, the code may be translated into a master task,
a slave task, or simply a non-parallel task to be used on serial and
vector machines. The master-slave communication is implemented by
message-passing calls (send/receives and broadcasts).
The k-point parallelization is not as trivial as it might seem
at first sight. Even though each iteration of the serial loop over
k-points is algorithmically independent of other iterations, the
wavefunction data actually depend crucially on the result of previous
iterations, when the standard Car-Parrinello iterative update of
wavefunctions takes place. When the k-points are updated in parallel with
the same initial potential, one may experience slowly converging or
even unstable calculations for systems with a significant
density-of-states at the Fermi level.
One can understand this behavior by considering the screening effects
that take place during an update of the electronic wavefunction: The
electrons will tend to screen out any non-selfconsistency in the
potential. When a standard algorithm loops serially through k-points ,
the first k-point will screen the potential as well as possible, the
second one will screen the remainder, and so on, leading to an
iterative improvement in the selfconsistency. However, when all
k-points are calculated from the same initial potential and in parallel,
they will all try to screen the same parts of the potential, leading to
an over-screening that gets worse with increasing numbers of processors,
possibly giving rise to an instability.
Obviously, some kind of ``damping'' of the over-screening is needed in
order to achieve a stable algorithm. We have selected the
following approach: Each k-point contains a number of electronic bands
(eigenstates), which are updated band by band using the conjugate
gradients method. The screening of the potential takes place through
the Coulomb and LDA exchange-correlation potentials derived from the
total charge density. We construct the total charge density and the
screening potentials after the update of each band (performed for all
k-points in parallel): When all processors have updated band no. 1, the
charge density and potentials are updated before proceeding to band no.
2, etc. This damping turns out to very effectively stabilize the
selfconsistency process, even for difficult systems such as Ni with
many states near the Fermi level.
The algorithmic difference may be summarized by the following
pseudo-code. The standard serial algorithm is:
DO k-point = 1, No_of_points
DO band = 1, No_of bands
Update wavefunction(k-point,band)
Calculate new charge density and screening potentials
END DO
END DO
whereas our parallel algorithm is:
DO band = 1, No_of bands
DO (in parallel) k-point = 1, No_of_points
Update wavefunction(k-point,band)
END DO
Calculate new charge density and screening potentials
END DO
It is understood that an outer loop controls the iterations towards a
selfconsistent solution. The conjugate gradient algoritm actually
requires the calculation of an intermediate ``trial'' step in the
wavefunction update, so that the work inside the outer loop is actually
twice that indicated in the pseudo-code. In addition, the subspace
rotations (not shown here) also require updates of the charge density.



Next: Results on IBM
Up: Parallel ab-initio molecular dynamics
Previous: Car-Parrinello ab-initio molecular
Ole Holm Nielsen
Thu Aug 24 12:01:50 MET DST 1995
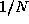 -th of the k-points ). The
wavefunction memory size is usually the limiting factor in
Car-Parrinello calculations. A number of tasks are not inherently
parallel: a) Input and output of wavefunctions and other data from a
standard data file, b) accumulation of k-point -dependent quantities such
as charge densities, eigenvalues, etc., c) the calculation of total
energy and forces, and the update of atomic positions, and d) analysis
of data depending only upon the charge density. These tasks should be
done by a ``master'' task.
-th of the k-points ). The
wavefunction memory size is usually the limiting factor in
Car-Parrinello calculations. A number of tasks are not inherently
parallel: a) Input and output of wavefunctions and other data from a
standard data file, b) accumulation of k-point -dependent quantities such
as charge densities, eigenvalues, etc., c) the calculation of total
energy and forces, and the update of atomic positions, and d) analysis
of data depending only upon the charge density. These tasks should be
done by a ``master'' task.