


Next: Conclusions
Up: Parallel ab-initio molecular dynamics
Previous: A parallel Car-Parrinello
The parallel algorithm described above is implemented in our
code using the Parallel Virtual Machine (PVM) message-passing
library, specifically the IBM PVMe implementation on the IBM SP2.
At the time this work was carried out, PVMe was the most efficient
message-passing library available from IBM, but we envisage
other libraries to be substituted easily for PVM with time,
or when porting to other parallel supercomputers such as the
Fujitsu VPP-500.
In order to show the performance of the k-point -parallel algorithm, we
choose a problem similar to a typical production problem of current
interest to us. We perform fully selfconsistent calculations of a slab
of a NiAl crystal with a (110) surface and a vacuum region, with 4
atoms in the unit cell. The plane wave energy cutoff was 50 Ry. We
choose a Brillouin-zone integration with 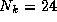 k-points so that an
even distribution of k-points over processors means that the job can be
run on
k-points so that an
even distribution of k-points over processors means that the job can be
run on 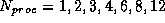 and 24 processors,
respectively. At each k-point
and 24 processors,
respectively. At each k-point 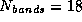 electronic bands were
calculated, and the charge density array had a size of (16,24,96), or
electronic bands were
calculated, and the charge density array had a size of (16,24,96), or
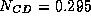 Mbytes. Only a single conjugate gradient step
(
Mbytes. Only a single conjugate gradient step
(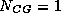 ) is used. The starting point was chosen to be a
selfconsistent NiAl system, where one of the Al atoms was subsequently
moved so that a new selfconsistent solution must be found.
) is used. The starting point was chosen to be a
selfconsistent NiAl system, where one of the Al atoms was subsequently
moved so that a new selfconsistent solution must be found.
In our parallel algorithm, after each band has been updated by the
slaves, the charge density array needs to be summed up from slaves to
the master task, and subsequently broadcast to all slaves. Since the
charge density array is typically 0.5 to 5 Mbytes to be communicated in
a single message, our algorithm requires the parallel computer to have
a high communication bandwidth and preferably support for global sum
operations. Communications latency is unimportant, at the level
provided on the IBM SP2.
Using the IBM PVMe optimized PVM version 3.2 library, a few minor
differences between PVMe and PVM 3.3 are easily coded around.
Unfortunately, the present PVMe release (1.3.1) lacks some crucial
functions of PVM 3.3: The pvm_psend pack-and-send optimization,
and the pvm_reduce group reduction operation, which could be
implemented as a binary tree operation similar to the reduction
operations available on the Connection Machines. Both would be very
important for optimizing the accumulation of the charge density array
from all slave tasks onto the master task; fortunately, they are
included in a forthcoming release of PVMe.
The estimated number of bytes exchanged between the master and all of
the slaves per iteration is
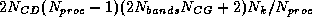 ,
or
,
or 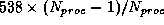 Mbytes total for the present
problem, ignoring the communication of smaller data arrays. Since the
IBM PVMe library doesn't implement reduction operations, the charge
density has to be accumulated sequentially from the slaves. IBM doesn't
document whether the PVMe broadcast operation is done sequentially or
using a binary tree, so we assume that the data is sent sequentially to
each of the slaves. If we take the maximum communication bandwidth
of an SP2 node with TB2 adapters to be B = 35 Mbytes/sec,
we have an estimate of the communication time as
Mbytes total for the present
problem, ignoring the communication of smaller data arrays. Since the
IBM PVMe library doesn't implement reduction operations, the charge
density has to be accumulated sequentially from the slaves. IBM doesn't
document whether the PVMe broadcast operation is done sequentially or
using a binary tree, so we assume that the data is sent sequentially to
each of the slaves. If we take the maximum communication bandwidth
of an SP2 node with TB2 adapters to be B = 35 Mbytes/sec,
we have an estimate of the communication time as
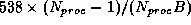 seconds per iteration.
seconds per iteration.
The runs were done at the UNI C 40--node SP2,
where for practical reasons we limited ourselves to up to 12 processors.
The timings for a single selfconsistent iteration over all k-points is
shown in Table 1, including the speedup relative to a single processor
with no message-passing. Since the number of subspace
rotations[7] varies depending on the wavefunction data, the
calculation of k-points may take different amounts of time so that some
processors will finish before others. The resulting
load-imbalance is typically of the order of 10%. We show the average
iteration timings in the table.
C 40--node SP2,
where for practical reasons we limited ourselves to up to 12 processors.
The timings for a single selfconsistent iteration over all k-points is
shown in Table 1, including the speedup relative to a single processor
with no message-passing. Since the number of subspace
rotations[7] varies depending on the wavefunction data, the
calculation of k-points may take different amounts of time so that some
processors will finish before others. The resulting
load-imbalance is typically of the order of 10%. We show the average
iteration timings in the table.

Table 1. Time for a single selfconsistent iteration, and the
speedup as a function of the number of processors.
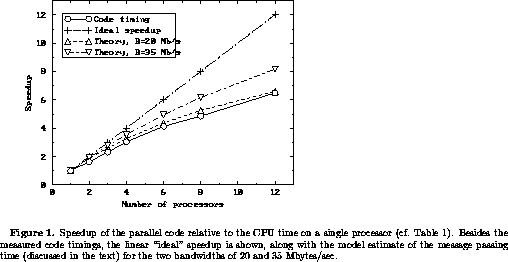
The speedup data is displayed in Fig. 1 together with the ``ideal''
speedup assuming an infinitely fast communication subsystem. More
realistically, we include the above estimate of the communication time
in the parallel speedup for the two cases of B = 20 and B = 35
Mbytes/sec, respectively. We see that the general shape of the
theoretical estimates agree well with the measured speedups, and that a
value of the order of B = 20 Mbytes/sec for the IBM SP2 communication
bandwidth seems to fit our data well. This agrees well with other
measurements[12] of the IBM SP2's performance using PVMe.
From the above discussion it is evident that any algorithmic
changes which would reduce the number of times that the charge density
needs to be communicated, while maintaining a stable algorithm, would
be most useful. We intend to pursue such a line of investigation.
Better message passing performance could be achieved by optimizing
carefully the operations that are used to communicate, mainly, the
electronic charge density. Efficient binary tree implementations of
the global summation as well as the broadcast of the charge density
should be made available in the message passing library, or could be
hand-coded into our application if unavailable in the library.



Next: Conclusions
Up: Parallel ab-initio molecular dynamics
Previous: A parallel Car-Parrinello
Ole Holm Nielsen
Thu Aug 24 12:01:50 MET DST 1995
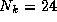 k-points so that an
even distribution of k-points over processors means that the job can be
run on
k-points so that an
even distribution of k-points over processors means that the job can be
run on 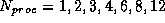 and 24 processors,
respectively. At each k-point
and 24 processors,
respectively. At each k-point 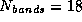 electronic bands were
calculated, and the charge density array had a size of (16,24,96), or
electronic bands were
calculated, and the charge density array had a size of (16,24,96), or
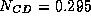 Mbytes. Only a single conjugate gradient step
(
Mbytes. Only a single conjugate gradient step
(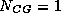 ) is used. The starting point was chosen to be a
selfconsistent NiAl system, where one of the Al atoms was subsequently
moved so that a new selfconsistent solution must be found.
) is used. The starting point was chosen to be a
selfconsistent NiAl system, where one of the Al atoms was subsequently
moved so that a new selfconsistent solution must be found.
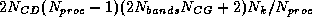 ,
or
,
or 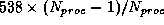 Mbytes total for the present
problem, ignoring the communication of smaller data arrays. Since the
IBM PVMe library doesn't implement reduction operations, the charge
density has to be accumulated sequentially from the slaves. IBM doesn't
document whether the PVMe broadcast operation is done sequentially or
using a binary tree, so we assume that the data is sent sequentially to
each of the slaves. If we take the maximum communication bandwidth
of an SP2 node with TB2 adapters to be B = 35 Mbytes/sec,
we have an estimate of the communication time as
Mbytes total for the present
problem, ignoring the communication of smaller data arrays. Since the
IBM PVMe library doesn't implement reduction operations, the charge
density has to be accumulated sequentially from the slaves. IBM doesn't
document whether the PVMe broadcast operation is done sequentially or
using a binary tree, so we assume that the data is sent sequentially to
each of the slaves. If we take the maximum communication bandwidth
of an SP2 node with TB2 adapters to be B = 35 Mbytes/sec,
we have an estimate of the communication time as
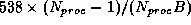 seconds per iteration.
seconds per iteration.
 C 40--node SP2,
where for practical reasons we limited ourselves to up to 12 processors.
The timings for a single selfconsistent iteration over all k-points is
shown in Table 1, including the speedup relative to a single processor
with no message-passing. Since the number of subspace
rotations[
C 40--node SP2,
where for practical reasons we limited ourselves to up to 12 processors.
The timings for a single selfconsistent iteration over all k-points is
shown in Table 1, including the speedup relative to a single processor
with no message-passing. Since the number of subspace
rotations[
