My main research interests are computational materials science, in particular the properties of nanoclusters and nanocrystalline metals. My main tool is molecular dynamics simulations, and I spend a significant part of my time on maintaining and developing computational software. I am heading the theory group of the research center CINF (Center for Individual Nanoparticle Functionality), funded by the Danish National Research Foundation (Grundforskningsfonden).


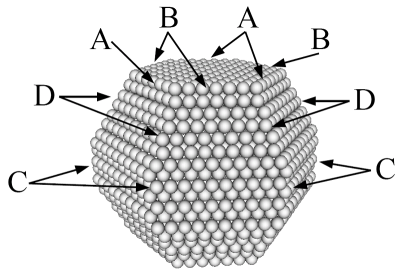
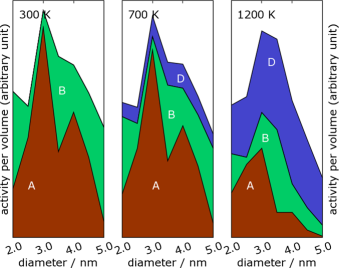
Left: A ruthenium cluster with special sites along the edges marked. The reactive sites are not the configurations shown, but the configurations that appear if a corner atom is removed at the marked sites.. Right: The contribution from these special sites to the reactivity of the cluster as a catalyst for the ammonia synthesis.
Nanoparticles have long been used in catalysts as a way to increase the surface area of the catalyst. However, nanoparticles are not just small particles and a good way to increase the surface-to-volume ratio, nanoparticles can have physical and chemical properties that differ significantly from the bulk material and from macroscopic surfaces. Confinement of the electrons in a nanoparticle may for example influence its properties. The curvature of the surface will change the kinds of surface sites where a chemical reaction could occur. It is already known that many reactions occur at surface steps, where a small molecule can bind to more surface atoms (at the bottom of a step a molecule may bind to five atoms instead of three or four on a flat surface). In CINF, we combine experiments and theory to study the relationship between shape and reactivity of nanoparticles.
Calculating the reactivity of a nanocluster is a two-step process. First, the shape of the cluster at a given temperature should be calculated, possibly including thermal fluctuations in the shape. Then the reactivity can be calculated by finding the densities of various types of active sites, and calculate their activities using quantum mechanical calculations. In principle, the shape could be found by running a Monte Carlo (MC) or molecular-dynamics (MD) simulation for a sufficiently long time. However, the equilibration times are too long for conventional simulation techniques, because there often are configurations of rather different shape that have similar energy.
My student, Jeppe Gavnholt, has developed a method where the cluster is described at two levels. A few "macroscopic" parameters describe the size and shape of the cluster. This description is augmented with a microscopic description of exactly where atoms are sitting. In this way, it is possibly to search out the relevant parts of configuration space in a computationally efficient way.
This paper illustrates how molecular dynamics simulations of particle shape can be combined with quantum mechanical calculations of reactivity, albeit in a different setting (electrochemistry) from the one discussed above.
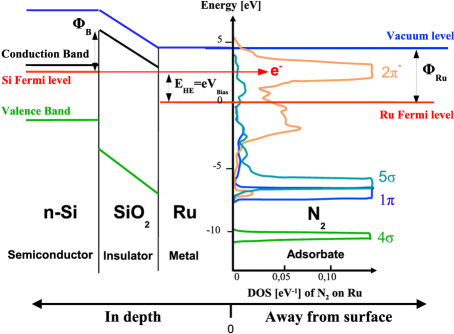
To cause a chemical reaction, energy is usually added in form of heat. In this way energy is added equally to all degrees of freedom in the system (the equipartition theorem). Hot-electron assisted surface chemistry is an attempt to add the energy only to a few degrees of freedom, for example the reaction coordinate. The basic principle is illustrated in the figure: A silicon-oxide-metal nanodevice is used to create ballistic electrons with an energy a few electron volts above the Fermi levels. If the voltage across the device is tuned so the energy of the hot electron matches an unoccupied (anti-bonding) molecular level of an adsorbed molecule, the chemical bond is weakened and energy is transferred to the molecule as a vibration, possibly leading to desorption or dissociation of the molecule. The same effect can not be obtained using electrons aimed at the surface from the vacuum side, as the relevant level of the adsorbed molecule typically lie below the vacuum level. Popularly speaking, an incoming electron would be attracted by the surface and accellerated to too high an energy before hitting the molecule.
The life time of the excited state thus created in the adsorbed molecule is very short due to the strong coupling to the surface, typically of the order of a femtosecond. This is too short to impart any significant energy to the molecule in a classical model, but the motion of the atoms is not classical. We have developed a quantum model describing the adsorbed molecule as a harmonic oscillator displaced by the occupation of the molecular state, and coupled to the conductance electrons of the metal. This model can be solved, and show a far greater transfer of energy than a classical model, predicting that it should be possible to desorb certain molecules with the hot electrons. This is currently being tested by one of the experimental groups in CINF.
The theoretical methods used to describe the specific systems are described in the next section.
In a collaboration with Kristian Thygesen at CAMD, we are starting a project investigating how to switch the conformation of a molecular junction in order to control the conductivity with optical or electrical pulses. Such a controllable molecular switch would be an important step towards developing molecular electronics.
Further information about the project can be found here: molecularelectronics_web.pdf
The "workhorse of quantum chemistry", Density Functional Theory (DFT), is a way to calculate the ground state electronic structure of a system. By construction, DFT is a ground state method and therefore not applicable to systems in electronically excited states such as the molecules discussed in the previous section. However, there exist extensions to DFT that can handle excited states, although they have a weaker theoretical foundation than DFT itself. We use Delta Self-Consistent Field (DSCF) and Time Dependent Density Functional Theory (TDDFT) in our group.
In its simplest form, DSCF consists of identifying the Kohn-Sham state with the greatest overlap with the desired excitation, and then keeping this state occupied during the self-consistency cycle of the DFT calculation. This method works well for undegenerate states in isolated molecules, but degeneracies lead to severe convergence problems. Worse, in the systems of interest to us, the interesting molecular state (typically the lowest unoccupied anti-bonding state) is coupled to the metallic states of the surface, turning it into a relatively broad resonance. In a DFT calculation, a significant number of Kohn-Sham states have a large overlap with the resonance - more so if the system size is increased. It is thus difficult to unambiguously identify which Kohn-Sham state to occupy, and the chosen state will only be partly localized on the molecule, leading to low occupation of the interesting state.
We have extended DSCF to handle this situation by instead occupying a linear combination of Kohn-Sham orbitals found by expanding the interesting molecular orbital on the Kohn-Sham states. This turns DSCF into a powerful method for this kind of problems. We benchmarked the method against more accurate calculations of excited states in molecules, and against inverse photoemission spectra of molecules adsorbed on metal surfaces, giving excellent agreement in spite of (or perhaps because of !) the simplicity of the DSCF method.
Time Dependent Density Functional Theory is a method where the density of a general state is evolved in time. TDDFT is thus not limited to ground state properties. The price is that the exchange-correlation kernel is no longer local in time, but depends on the density at all previous times. This difficulty is usually ignored, leading to adiabatic TDDFT, an approximation closely related to DSCF.
We use adiabatic TDDFT to study the interaction between an incoming hot electron and an adsorbed molecule, i.e. the excitation event leading to the excited state then studied with DSCF. We have also been studying the decay of the excited state.
The atomic-scale processes determining the mechanical properties of metals and metallic systems have long been one of my main research interests. The research has been focused on the mechanical properties of nanocrystalline metals and metallic glasses.
To be written ....
To be written ....